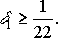Анализ на чувствительность с помощью двойственной задачи
Определение двойственной задачи.
Прямая задача ЛП в стандартной форме записывается следующим образом:
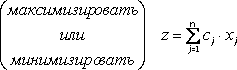
при ограничениях:
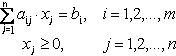
Заметим, что в состав n переменных включаются также избыточные и остаточные переменные.
Дадим определение двойственной задачи.
Двойственная задача - это вспомогательная задача ЛП, формулируемая с помощью определенных правил непосредственно из условий исходной, или прямой, задачи. В литературе по ЛП в большинстве случаев рассматриваются формулировки двойственной задачи, соответствующие различным формам прямой задачи, которые в свою очередь определяются типом ограничений, знаками переменных и направлением оптимизации (максимизация или минимизация). Однако, практическое использование теории двойственности на самом деле не требует знания деталей различных формулировок двойственной задачи.
Приведем обобщенную формулировку двойственной задачи ЛП, которая применима к любой форме представления прямой задачи. В основу такой формулировки положен тот факт, что использование симплекс-метода требует приведения любой задачи ЛП к стандартной форме. Следует, однако, помнить, что приводимая ниже формулировка двойственной задачи является обобщенной в том смысле, что она применима ко всем формам прямой задачи.
Двойственная задача получается путем симметричного структурного преобразования условий прямой задачи в соответствии со следующими правилами:
- Каждому ограничению прямой задачи соответствует переменная двойственной задачи;
- Каждой переменной прямой задачи соответствует ограничение двойственной задачи;
- Коэффициенты при некоторой переменной, фигурирующие в ограничениях прямой задачи, становятся коэффициентами левой части соответствующего ограничения двойственной задачи, а коэффициенты, фигурирующие при той же переменной в выражении для целевой функции прямой задачи, становится постоянной правой частью этого же ограничения двойственной задачи.
Из указанных правил построения двойственной задачи следует, что она имеет m переменных (y1, y2, …, ym) и n ограничений (соответствующих n переменным прямой задачи x1, x2, …, xn).
Рассмотрим теперь, как формируются остальные условия двойственной задачи: направление оптимизации, ограничения и знаки двойственных переменных.

Прямая задача в стандартной форме - это задача, в которой все ограничения - равенства с неотрицательными правыми частями, а все переменные неотрицательные. Поэтому существенным различием прямых задач, записанных в стандартной форме, является только направление оптимизации.
Рассмотрим пример построения двойственной задачи, имея математическую модель прямой задачи, покажем зависимость между ними.
Рассмотрим в качестве примера задачу о рекламе:
Фирма имеет возможность рекламировать свою продукцию, используя местные радио- и телевизионную сети. Затраты на рекламу в бюджете фирмы ограничены величиной 1000$ в месяц. Каждая минута радиорекламы обходится в 5$, а каждая минута телерекламы - в 100$. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения, но при этом фирма решила, что время радиорекламы не должно превышать двух часов. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определите оптимальное распределение финансовых средств, ежемесячно отпускаемых на рекламу, между радио- и телерекламой.
Решение: Обозначим за хТ - количество финансовых средств, отпускаемых на телерекламу, а за хР - количество финансовых средств, отпускаемых на радиорекламу. Сразу же можем записать одно ограничение на общее количество средств, отпускаемых на рекламу:
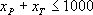
Количество минут, используемых для рекламы на радио, будет вычисляться следующим обра
зом:
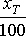 , а количество минут, используемых для рекламы на телевидении :
, а количество минут, используемых для рекламы на телевидении :
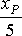
Для простоты будем считать, что время на рекламу можно покупать посекундно.
Условие использования радиосети по крайней мере в два раза чаще, чем сеть телевидения, запишется следующим ограничением:
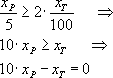
Решение о том, что время радиорекламы не должно превышать двух часов, запишется в виде:
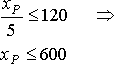
А теперь запишем целевую функцию. По условию задачи мы должны найти оптимальное значение распределения финансовых средств, чтобы эффективность от рекламы была максимальной. Если эффективность одной минуты радиорекламы обозначить за единицу, то эффективность одной минуты телерекламы будет равна двадцатипяти. Получим следующую функцию:
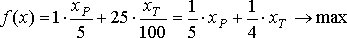
Из условия задачи естественно вытекают ещё два ограничения:
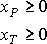
Сведем все ограничения и целевую функцию в одну систему:
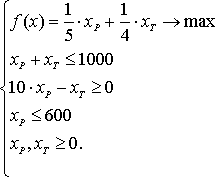
Приведем систему к стандартному виду и учтем тот факт, что симплекс-метод используется для системы, которую надо минимизировать.
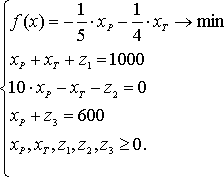
Возьмем в качестве свободных переменных хТ и хР, а в качестве базисных примем z1, z2 и z3, умножив при этом второе ограничение на -1. Составим начальную симплекс-таблицу и решим систему.

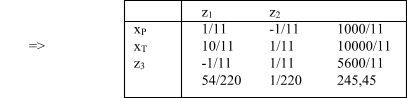
Таким образом, получили, что на радиорекламу надо тратить 90,90$, а на телерекламу - 909,09$, что в минутах составляет на радио - 18,18 минуты, а на телевидении - 9,9 минуты. Тот же результат можно получить и графически.
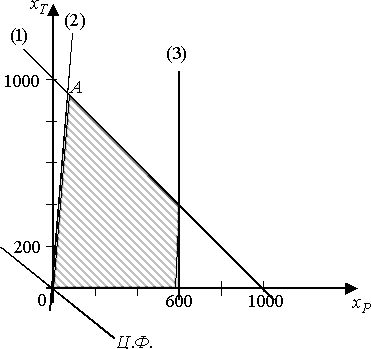
Точка А соответствует оптимуму системы уравнений.
Теперь перейдем от прямой задачи к двойственной.
Обозначим переменные двойственной задачи за y1, y2, y3, т. е. количество переменных равно количеству ограничений в прямой задаче. При этом переменные двойственной задачи считаются неограниченными по знаку. Поставим каждому ограничению прямой задачи переменную из двойственной.
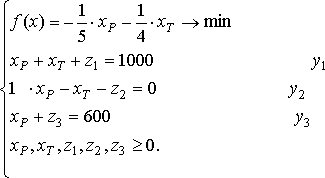
Теперь составим целевую функцию двойственной задачи.
Значения при переменных в целевой функции берутся из правых частей ограничений прямой задачи, при этом рядом каким-либо значением ставится та переменная, которая соответствует данному ограничению. Направление улучшения целевой функции двойственной задачи противоположно направлению улучшения целевой функции прямой задачи.
Получим:
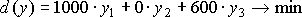
Теперь каждому ограничению двойственной задачи поставим в соответствие переменную прямой задачи. Т. е. будем считать, что первому ограничению двойственной задачи соответствует, например, переменная хР из прямой задачи. Получим следующее ограничение:
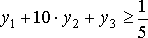
Обратим внимание на то обстоятельство, что в правой части ограничения стоит значение при хР из целевой функции прямой задачи.
Таким же образом составим остальные ограничения для двойственной задачи, которым будут соответствовать переменные хТ, z1, z2, z3 из прямой задачи. Необходимо отметить тот факт, что порядок выбора переменных прямой задачи для составления ограничений двойственной произволен и не влияет на решение задачи, а будет влиять лишь на расположения ограничений в задаче.
Собрав все полученные ограничения, мы можем записать:
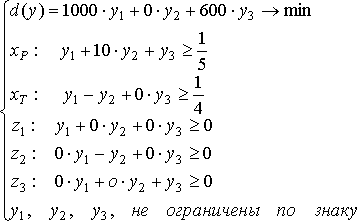
Из третьего, четвертого и пятого ограничения видно, что последнее ограничение избыточно. Избавившись от избыточности, получим следующий вид двойственной задачи:
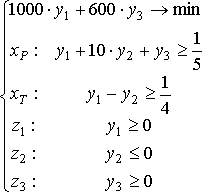
Теперь эту задачу можно решать как прямую, т.е. сначала ее необходимо перевести в задачу стандартного вида, затем построить начальную симплекс-таблицу и решить задачу симплекс-методом.
Решение: Приведем задачу к стандартному виду:
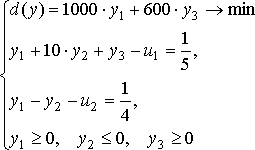
Решим систему симплекс-методом. Возьмем в качестве базисных переменных переменные y3 и -y2. Выведем y3 из целевой функции и y2 из первого ограничения. Для этого выразим y2 из второго ограничения, подставим его в первое. Затем из первого уравнения выразим y3, и подставим в целевую функцию. В итоге получим:
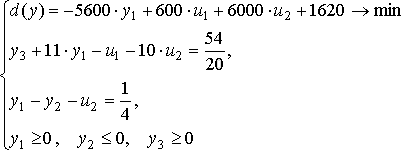

Получаем следующее оптимальное решение двойственной задачи:
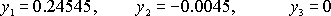
Далее будет показано, что между прямой и двойственной задачами существует тесная взаимосвязь. Фактически, имея оптимальную симплекс-таблицу одной задачи, можно получить оптимальное решение другой, не производя громоздких вычислений и не используя симплекс-метод. Заинтересованность в определении оптимального решения прямой задачи путем решения двойственной к ней задачи обусловлена тем, что вычисления, необходимые для решения двойственной задачи, могут оказаться менее сложными, чем для прямой задачи. Напомним, что трудоемкость вычислений при решении задач ЛП в большей степени зависит от числа ограничений, чем от количества переменных. Поэтому, если в двойственной задаче ограничений меньше, чем в прямой, как правило, целесообразнее решать двойственную задачу и полученный результат использовать для нахождения оптимального решения прямой задачи.
Оптимальное решение прямой задачи можно получить непосредственно из симплекс-таблицы для двойственной задачи, если воспользоваться следующим уравнением:

Покажем, что оптимальное решение прямой задачи в свою очередь так же непосредственно определяется из симплекс-таблицы для оптимального решения двойственной задачи.
Заметим, что переменные xP и хТ связаны с первым и вторым ограничениями двойственной задачи соответственно и, следовательно, с искусственными переменными u1 и u2.
 (**)
(**)
Следовательно,
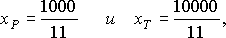
Таким образом, получим тот же результат, который приведен в симплекс-таблице для оптимального решения прямой задачи.
Анализ сопоставления результатов, полученных при решении прямой и двойственной задачи, позволяет сформулировать интересный вывод.
На итерации, приводящей к оптимуму,
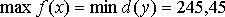
Это равенство справедливо всегда и фактически соответствует оптимальным значениям переменных обеих задач.
Интерпретация симплекс-таблиц.
Исследователя вряд ли устроила бы заключительная симплекс-таблица, из которой можно было бы получить только список переменных и их значения. На самом деле результирующая симплекс-таблица насыщена весьма важными данными, лишь небольшую часть которых составляют оптимальные значения переменных. Из симплекс-таблицы можно получить информацию об:
- оптимальном решении
- статусе ресурсов
- ценности каждого ресурса
- чувствительности оптимального решения к изменению запасов ресурсов, вариациям коэффициентов целевой функции и интенсивности потребления ресурсов.
Возьмём для примера заключительную симплекс-таблицу прямой задачи.
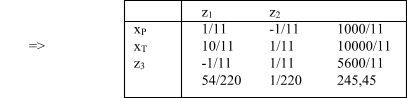
Те переменные, которые не присутствуют в базисе, обязательно имеют нулевое значение. Т. о. оптимальное решение имеет вид
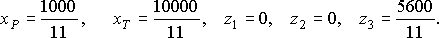
Теперь рассмотрим ресурсы. Говоря о ресурсах, мы подразумеваем, что установлены некоторые максимальные пределы их запасов, поэтому в соответствующих исходных ограничениях должен использоваться знак
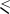 . Следовательно, ограничения со знаком
. Следовательно, ограничения со знаком
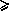 не могут рассматриваться как ограничения на ресурсы. Статус ресурсов (дефицитный или недефицитный) можно непосредственно узнать из результирующей симплекс-таблицы, обращая внимание на значения остаточных переменных.
Положительно значение остаточной переменной указывает на неполное использование соответствующего ресурса, т.е. ресурс недефицитный. Если же остаточная переменная равна нулю, это свидетельствует о полном потреблении данного ресурса.
не могут рассматриваться как ограничения на ресурсы. Статус ресурсов (дефицитный или недефицитный) можно непосредственно узнать из результирующей симплекс-таблицы, обращая внимание на значения остаточных переменных.
Положительно значение остаточной переменной указывает на неполное использование соответствующего ресурса, т.е. ресурс недефицитный. Если же остаточная переменная равна нулю, это свидетельствует о полном потреблении данного ресурса.
В нашей задаче ограничениями на ресурсы будут первое и третье ограничения.
Остаточная переменная z1=0, следовательно, максимальное количество отпускаемых денежных средств на рекламу - это дефицитный ресурс. А переменная z3 = 5600/11, следовательно, ограничение на использование радио не больше двух часов недефицитный ресурс. Это же можно увидеть и из рисунка. Перемещая прямую (1), мы получим другое оптимальное решение. Перемещение же прямой (3) до определенного уровня не отразиться на оптимальном решении.
Ценность ресурса характеризуется величиной улучшения оптимального значения f(x), приходящегося на единицу прироста объема данного ресурса. Ценность ресурсов всегда можно определить по значениям коэффициентов при остаточных переменных, фигурирующих в f(x)-уравнении оптимальной симплекс-таблицы. Возвращаясь к нашему примеру: ценность первого ресурса равна 54/220. Отсюда следует, что увеличение переменной z1 приведет к пропорциональному увеличению значения целевой функции с коэффициентом пропорциональности 54/220. То же самое можно сказать и об уменьшении переменной z1.
Замечание: При характеристике ценности ресурсов экономисты предпочитают использовать такие термины, как теневая цена, скрытая цена, или более специфичный термин - двойственная оценка.
Максимальное изменение запаса ресурсов.
При решении вопроса о том, запас какого из ресурсов следует увеличивать в первую очередь, обычно используют теневые цены. Чтобы определить интервал значений изменения запаса ресурса, при которых теневая цена данного ресурса, фигурирующая в заключительной симплекс-таблице, остается неизменной, необходимо выполнить ряд дополнительных вычислений. Рассмотрим сначала соответствующие вычислительные процедуры, а затем покажем, как требуемая информация могла быть получена из результирующей симплекс-таблицы.
Зададимся вопросом: как измениться результирующая симплекс-таблица при изменении запаса первого ресурса на
 .
Чтобы узнать это, изменим соответствующее ограничение. Оно будет иметь вид:
.
Чтобы узнать это, изменим соответствующее ограничение. Оно будет иметь вид:
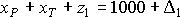
Оставим остальные условия без изменений и решим задачу симплекс-методом. Результаты представим в следующей таблице:

Эти же данные можно получить и из результирующей симплекс-таблицы. Заметим, что в каждой итерации новая правая часть представляет собой сумму двух величин: постоянной и члена, линейно зависящего от
 .
. Постоянные соответствуют числам, которые фигурируют на соответствующих итерациях в правых частях ограничений симплекс-таблиц до введения
.
. Постоянные соответствуют числам, которые фигурируют на соответствующих итерациях в правых частях ограничений симплекс-таблиц до введения
 .
. Коэффициенты при
.
. Коэффициенты при
 .
во вторых слагаемых равны коэффициентам при z1 на той же итерации, потому что эта переменная связана с первым ограничением.
.
во вторых слагаемых равны коэффициентам при z1 на той же итерации, потому что эта переменная связана с первым ограничением.
Выводы: т. к. введение
 .
сказывается лишь на правой части симплекс-таблицы, изменение запаса ресурса может повлиять только на допустимость решения. Следовательно, величина
.
сказывается лишь на правой части симплекс-таблицы, изменение запаса ресурса может повлиять только на допустимость решения. Следовательно, величина
 .
должна быть ограничена таким интервалом значений, при которых выполняется условие неотрицательности правых частей ограничений. Т. е.
.
должна быть ограничена таким интервалом значений, при которых выполняется условие неотрицательности правых частей ограничений. Т. е.
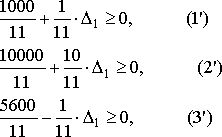
Для определения допустимого интервала изменения
рассмотрим два случая:
Случай 1:
 >0. Соотношение (1') и (2') всегда выполняются при
>0. Соотношение (1') и (2') всегда выполняются при
 >0. Соотношение (3') неотрицательно при
>0. Соотношение (3') неотрицательно при
 %lt= 5600.
%lt= 5600.
Случай 2:
 < 0. Соотношение (3') всегда выполняется. Соотношение(1') и (2') выполняется при
< 0. Соотношение (3') всегда выполняется. Соотношение(1') и (2') выполняется при
 => -1000.
=> -1000.
Обобщая результат, можно сделать вывод, что решение задачи всегда будет допустимым, если
 будет находиться в интервале [-1000, 5600].
будет находиться в интервале [-1000, 5600].
Максимальное изменение коэффициентов целевой функции
Также представляет интерес и установление интервала допустимых изменений коэффициентов целевой функции. Следует отметить, что уравнение целевой функции также никогда не используется в качестве ведущего уравнения. Поэтому любые изменения окажут влияние только на f(x)-уравнение результирующей симплекс-таблицы. Это означает, что такие изменения могут сделать полученное решение неоптимальным. Наша задача - найти интервалы значений изменений коэффициентов целевой функции (рассматривая каждый из коэффициентов отдельно), при которых оптимальные значения переменных остаются неизменными.
В нашем примере положим, что эффективность от использования телевидения изменилась на
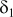 , где
, где
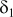 может быть и положительным и отрицательным числом. Целевая функция при этом имеет следующий вид:
может быть и положительным и отрицательным числом. Целевая функция при этом имеет следующий вид:
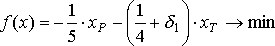
Выполнив все вычисления, необходимые для получения результирующей симплекс-таблицы, в f(x)-уравнении получим:
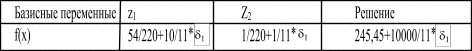
Это уравнение отличается от f(x)-уравнения до введения
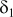 только наличием членов, содержащих
только наличием членов, содержащих
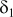 . Коэффициенты при
. Коэффициенты при
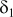 равны коэффициентам при соответствующих переменных в xТ строке результирующей симплекс-таблицы.
равны коэффициентам при соответствующих переменных в xТ строке результирующей симплекс-таблицы.
Оптимальные значения переменных будут оставаться неизменными при значениях
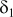 , удовлетворяющих условию неположительности (задача на отыскание минимума) всех коэффициентов при небазисных переменных в f(x)-уравнении. Т. о. должны выполняться следующие неравенства
, удовлетворяющих условию неположительности (задача на отыскание минимума) всех коэффициентов при небазисных переменных в f(x)-уравнении. Т. о. должны выполняться следующие неравенства
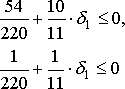
Из первого неравенства получаем
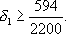 Из второго:
Из второго:
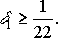
Т. е. при увеличении коэффициента при хТ в целевой функции на величину, превышающую 594/2200, оптимальные значения переменных останутся неизменными, но само значение функции будет меняться.
Такие же вычисления можно проделать и для переменной хР.
Заключение.
Имея оптимальную симплекс-таблицу прямой задачи можно узнать не только оптимальное решение задачи, но и оценить статус ресурсов и их ценность. Анализ модели на чувствительность выявляет определенный интервал изменения значений запасов ресурсов, при котором вид целевой функции остается неизменным. При анализе модели на чувствительность может быть определен также и некоторый интервал значений изменения коэффициентов целевой функции, при которых сохраняются полученные ранее оптимальные значения переменных. Но если решать прямую задачу очень сложно, то проще решить двойственную задачу. И имея оптимальную симплекс-таблицу двойственной задачи можно получить оптимальную симплекс-таблицу прямой задачи, не решая её.


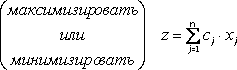
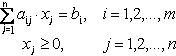

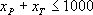
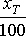 , а количество минут, используемых для рекламы на телевидении :
, а количество минут, используемых для рекламы на телевидении :
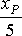
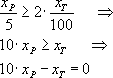
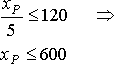
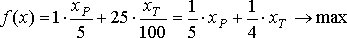
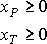
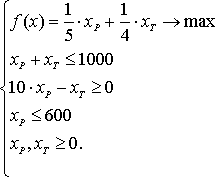
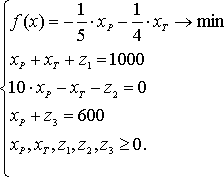

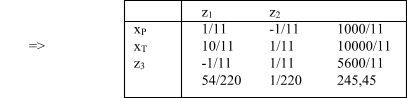

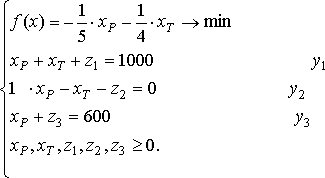
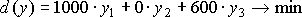
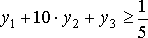
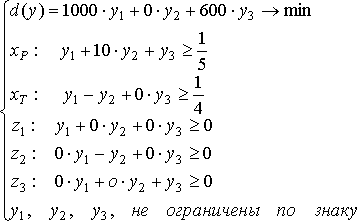
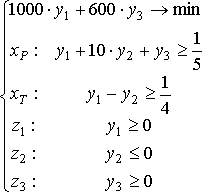
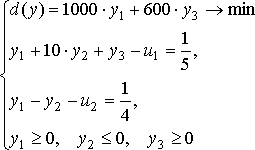
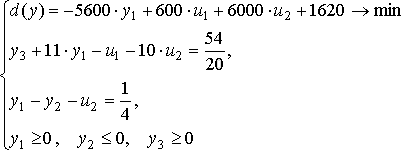

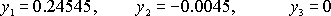

 (**)
(**)
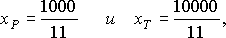
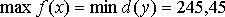
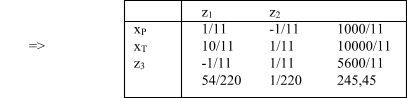
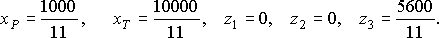
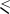 . Следовательно, ограничения со знаком
. Следовательно, ограничения со знаком
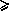 не могут рассматриваться как ограничения на ресурсы. Статус ресурсов (дефицитный или недефицитный) можно непосредственно узнать из результирующей симплекс-таблицы, обращая внимание на значения остаточных переменных.
Положительно значение остаточной переменной указывает на неполное использование соответствующего ресурса, т.е. ресурс недефицитный. Если же остаточная переменная равна нулю, это свидетельствует о полном потреблении данного ресурса.
не могут рассматриваться как ограничения на ресурсы. Статус ресурсов (дефицитный или недефицитный) можно непосредственно узнать из результирующей симплекс-таблицы, обращая внимание на значения остаточных переменных.
Положительно значение остаточной переменной указывает на неполное использование соответствующего ресурса, т.е. ресурс недефицитный. Если же остаточная переменная равна нулю, это свидетельствует о полном потреблении данного ресурса.
 .
Чтобы узнать это, изменим соответствующее ограничение. Оно будет иметь вид:
.
Чтобы узнать это, изменим соответствующее ограничение. Оно будет иметь вид:
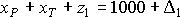

 .
. Постоянные соответствуют числам, которые фигурируют на соответствующих итерациях в правых частях ограничений симплекс-таблиц до введения
.
. Постоянные соответствуют числам, которые фигурируют на соответствующих итерациях в правых частях ограничений симплекс-таблиц до введения
 .
. Коэффициенты при
.
. Коэффициенты при
 .
во вторых слагаемых равны коэффициентам при z1 на той же итерации, потому что эта переменная связана с первым ограничением.
.
во вторых слагаемых равны коэффициентам при z1 на той же итерации, потому что эта переменная связана с первым ограничением.
 .
сказывается лишь на правой части симплекс-таблицы, изменение запаса ресурса может повлиять только на допустимость решения. Следовательно, величина
.
сказывается лишь на правой части симплекс-таблицы, изменение запаса ресурса может повлиять только на допустимость решения. Следовательно, величина
 .
должна быть ограничена таким интервалом значений, при которых выполняется условие неотрицательности правых частей ограничений. Т. е.
.
должна быть ограничена таким интервалом значений, при которых выполняется условие неотрицательности правых частей ограничений. Т. е.
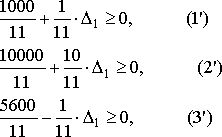
 >0. Соотношение (1') и (2') всегда выполняются при
>0. Соотношение (1') и (2') всегда выполняются при
 >0. Соотношение (3') неотрицательно при
>0. Соотношение (3') неотрицательно при
 %lt= 5600.
%lt= 5600.
 < 0. Соотношение (3') всегда выполняется. Соотношение(1') и (2') выполняется при
< 0. Соотношение (3') всегда выполняется. Соотношение(1') и (2') выполняется при
 => -1000.
=> -1000.
 будет находиться в интервале [-1000, 5600].
будет находиться в интервале [-1000, 5600].
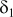 , где
, где
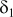 может быть и положительным и отрицательным числом. Целевая функция при этом имеет следующий вид:
может быть и положительным и отрицательным числом. Целевая функция при этом имеет следующий вид:
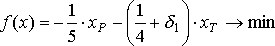
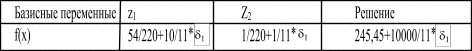
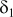 только наличием членов, содержащих
только наличием членов, содержащих
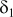 . Коэффициенты при
. Коэффициенты при
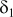 равны коэффициентам при соответствующих переменных в xТ строке результирующей симплекс-таблицы.
равны коэффициентам при соответствующих переменных в xТ строке результирующей симплекс-таблицы.
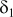 , удовлетворяющих условию неположительности (задача на отыскание минимума) всех коэффициентов при небазисных переменных в f(x)-уравнении. Т. о. должны выполняться следующие неравенства
, удовлетворяющих условию неположительности (задача на отыскание минимума) всех коэффициентов при небазисных переменных в f(x)-уравнении. Т. о. должны выполняться следующие неравенства
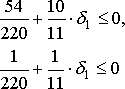
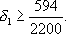 Из второго:
Из второго: