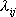Уравнения Колмогорова для вероятностей состояний.

При рассмотрении марковских процессов с дискретными состояниями и непрерывным временем будем считать, что все переходы некоторой системы из одного состояния в другое происходят под действием потоков событий. Если все потоки простейшие, то процесс протекающий в системе будет марковским. На графе состояний системы у каждой стрелки будем проставлять интенсивность потока событий

, переводящего систему из состояния

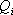в состояние

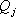(см. рис.5 ). Для рассмотренного ранее примера о техническом устройстве, состоящим из двух узлов размеченный граф показан на рис.5 .

Здесь

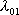- интенсивность потока отказов первого узла;

(

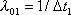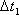- среднее время безотказной работы первого узла). Для размеченного графа показанного на рис. определим вероятности состояний системы

(

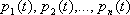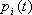- вероятность i-ого состояния системы,

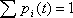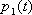Для этого составим систему уравнений Колмогорова для конкретной системы, Размеченный граф состояний которой показан на рисунке. Найдем вероятность

, что в момент t система будет находиться в состоянии

.
Придадим t приращение

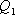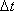и найдем вероятность того, что в момент

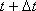система будет находиться в состоянии

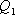. Это событие может осуществиться двумя способами:
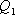1. В момент t система была в состоянии

и за время

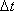из него не вышла;
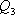2. В момент t система была в состоянии

и за

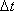перешла в

.
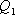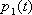Вероятность первого варианта равна произведению

на условную вероятность того, что за

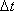не произойдет перехода

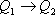. Эта вероятность равна

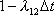. В итоге имеем

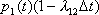. Вероятность второго варианта равна

(

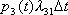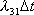- вероятность условного перехода

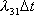). В итоге

.
Деля обе части на

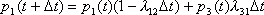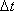и переходя к пределу при

найдем

Аналогично можно найти еще три уравнения

Эти уравнения называются уравнениями Колмогорова.
Интегрируя эту систему уравнений, найдем вероятности состояний, как функции времени.Для этого необходимо задать начальные условия при t=0.
Например

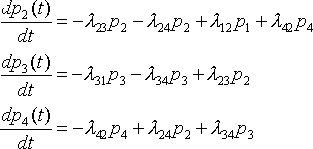
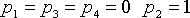- это означает, что при t=0 система находится в состоянии Q2.
Сформулируем правило составления дифференциальных уравнений:

в левой части каждого уравнения стоит производная вероятности состояния, а правая содержит столько членов, сколько стрелок связано с данным соcтоянием. Если стрелка направлена из состояния, соответствующий член имеет знак "-", если в состояние знак "+".
Каждый член равен произведению плотности вероятности перехода, соответствующему данной стрелке, умноженной на вероятность состояния, из которого исходит стрелка.