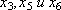Задачи линейного программирования.
Пример задачи о производстве красок
Задача фирмы Reddy Mikks
Небольшая фабрика фирмы Reddy Mikks изготовляет два вида красок: для внутренних (I) и наружных (E) работ. Продукция обоих видов поступает в оптовую продажу.
Для производства красок используются два исходных продукта-А и В. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 т соответственно. Расходы А и В на 1 т соответствующих красок и максимально возможный запас приведены в таблице.

Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску Е более чем на 1 т.
Кроме этого установлено, что спрос на краску I никогда не превышает 2 т в сутки.
Оптовые цены одной тонны красок равны:
3 тыс. долл. для краски Е
2 тыс. долл. для краски I.
Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
Построение математической модели
Процесс построения математической модели для решения поставленной задачи можно начать с ответов на три следующие вопроса:
- Для определения каких величин должна быть построена модель?
- Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, для моделируемой системы?
- В чем состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному (наилучшему) решению задачи?
Отвечая на поставленные вопросы сформулируем суть проблемы-фирме требуется определить объемы производства (в тоннах) каждой из красок,
который максимизирует доход (в тысячах долларов) от реализации продукции, с учетом ограничений на спрос и расход исходных продуктов.
Введем переменные:
так как нужно определить объемы производства каждого вида краски, то переменными в модели являются
xE - суточный объем производства краски Е (в тоннах)
xI - суточный объем производства краски I (в тоннах).
Так как стоимость 1 т краски Е равна 3 тыс. долл., суточный доход от ее продажи составит 3 xE тыс. долл. Аналогично доход от реализации xI тонн краски I составит 2 xI тыс. долл. в сутки. При допущении независимости объемов сбыта каждой из красок можно дать следующую математическую формулировку целевой функции: определить (допустимые) значения xЕ и xI, максимизирующие величину общего дохода
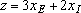
Ограничения:
При решении рассматриваемой задачи должны быть учтены ограничения на расход исходных продуктов и спрос на изготовляемые краски. Ограничение на расход исходных продуктов можно записать следующим образом:
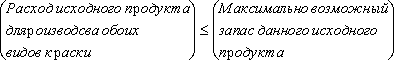
Это приводит к следующим двум ограничениям:
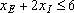 (для А)
(для А)
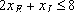 (для В)
(для В)
Ограничения на величину спроса красок имеют вид
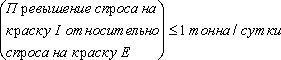
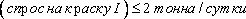
Эти ограничения имеют вид:
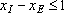 (соотношение величин спроса на краску I и краску Е),
(соотношение величин спроса на краску I и краску Е),
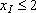 (максимальная величина спроса на краску I).
(максимальная величина спроса на краску I).
Переменные xI и xE не могут принимать отрицательных значений:
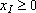 (объем производства краски I),
(объем производства краски I),
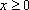 (объем производства краски Е).
(объем производства краски Е).
Итак, математическую модель можно записать следующим образом.
Определить суточные объемы производства (xI и xE ) краски I и краски Е (в тоннах), при которых достигается
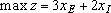 (целевая функция)
(целевая функция)
при ограничениях:
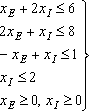
Что определяет линейный характер построенной модели? С формальных позиций данная модель является линейной потому, что все входящие в нее функции (ограничения и целевая функция) линейны. Линейность предполагает наличие двух свойств - пропорциональности и аддитивности.
- Пропорциональность означает, что вклад каждой переменной хЕ и хI в целевую функцию прямо пропорционален этим переменным.
- Аддитивность заключается в том, что целевая функция представляет собой сумму вкладов от различных переменных. Однако если фирма производит два конкурирующих вида продукции, увеличение сбыта одного из которых отрицательно сказывается на объеме реализации другого, то такая модель не обладает свойством аддитивности.
Транспортная задача
Имеются пункты (склады) П1,...,Пk хранения некоторого продукта, в каждом из которых содержится соответственно ai,...ak
единиц этого продукта, и пункты потребления Пi,...,Пk
получающие продукт в количествах
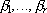 Запасы и потребности сбалансированы, т. е.
Запасы и потребности сбалансированы, т. е.
 и каждый
и каждый
 может взаимодействовать с каждым.
Стоимость перевозки единицы имеющегося продукта со склада
может взаимодействовать с каждым.
Стоимость перевозки единицы имеющегося продукта со склада
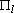 в пункт
в пункт
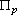 составляет clp.
составляет clp.
Если при этом количество перевозимого продукта есть xlp, то стоимость рассматриваемой "элементарной" операции оценивается величиной clpxlp, а общая стоимость всех перевозок - величиной
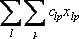 Требуется выбрать такие значения xlp, т. е. составить план перевозок, при которых суммарные затраты на транспортировку окажутся минимальными.
Требуется выбрать такие значения xlp, т. е. составить план перевозок, при которых суммарные затраты на транспортировку окажутся минимальными.
Математическая задача формулируется следующим образом:
найти
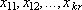 доставляющие минимум функции
доставляющие минимум функции
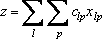 при ограничениях:
при ограничениях:
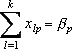 (каждый пункт потребления получает нужное количество продукта);
(каждый пункт потребления получает нужное количество продукта);
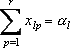 (каждый склад полностью освобождается);
(каждый склад полностью освобождается);
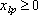 (объемы перевозок не могут быть отрицательными).
(объемы перевозок не могут быть отрицательными).
Основная задача линейного программирования (ОЗЛП) ставится следующим образом:
Имеется ряд переменных
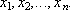 Требуется найти такие их неотрицательные значения, которые удовлетворяли бы системе линейных уравнений:
Требуется найти такие их неотрицательные значения, которые удовлетворяли бы системе линейных уравнений:
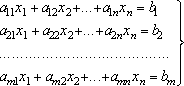 {1}
{1}
и, кроме того, обращали бы в минимум линейную функцию
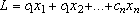 Очевидно, случай, когда линейную функцию нужно обратить не в минимум, а в максимум, легко сводится к предыдущему, если изменить знак функции и рассмотреть вместо нее функцию
Очевидно, случай, когда линейную функцию нужно обратить не в минимум, а в максимум, легко сводится к предыдущему, если изменить знак функции и рассмотреть вместо нее функцию
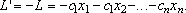 Оптимальным решением будем называть то из допустимых решений, при котором линейная функция обращается в минимум.
Оптимальным решением будем называть то из допустимых решений, при котором линейная функция обращается в минимум.
Основная задача линейного программирования (ОЗЛП) необязательно должна иметь решение. Может оказаться, что уравнения (1) противоречат друг другу, может оказаться, что они имеют решение, но в области отрицательных значений х1,х2,...,xn
Тогда ОЗЛП не имеет допустимых решений. Может оказаться, что допустимые решения ОЗЛП существуют, но среди них нет оптимального: функция L в области допустимых решений неограничена снизу.
Условимся называть допустимым решением ОЗЛП любую совокупность переменных
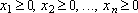 удовлетворяющую уравнениям (1).
удовлетворяющую уравнениям (1).
Оптимальным решением будем называть то из допустимых решений, при котором линейная функция обращается в минимум.
На практике ограничения в задаче линейного программирования часто заданы не уравнениями, а неравенствами. В этом случае можно перейти к основной задаче линейного программирования.
Рассмотрим задачу линейного программирования с ограничениями-неравенствами, которые имеют вид
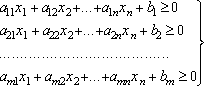
и являются линейно-независимыми. Последнее означает, никакое из них нельзя представить в виде линейной комбинации других.
Требуется найти
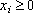 которые удовлетворяют неравенствам и обращают в минимум
которые удовлетворяют неравенствам и обращают в минимум
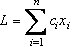 {2}
{2}
Введём уравнения:
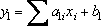
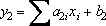 {3}
{3}
..............
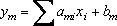
где y1,y2,...,ym - добавочные переменные, которые также как и x1,x2,...xn являются неотрицательными.
Таким образом имеем общую задачу линейного программирования - найти неотрицательные
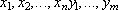 чтобы они удовлетворяли системе уравнений (3) и обращали в минимум
чтобы они удовлетворяли системе уравнений (3) и обращали в минимум
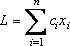 Коэффициенты в формуле (2) перед yj равны нулю.
Коэффициенты в формуле (2) перед yj равны нулю.
Рассмотрим графическое решение задачи о производстве красок. Такая возможность связана с тем, что здесь только две переменные
Первый шаг при использовании графического метода заключается в построении области допустимых решений, в которой одновременно выполняются все ограничения модели.
Искомая область (пространство) решений показана на рис. 1.
Условия неотрицательности переменных
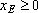 и
и
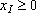 ограничивают область их
допустимых значений первым квадрантом.
ограничивают область их
допустимых значений первым квадрантом.
Другие границы пространства решений изображены на плоскости xE,xI прямыми линиями, построенными по уравнениям, которые получаются при замене в ограничениях знаков неравенства на знаки равенства.
Области, в которых выполняются соответствующие ограничения в виде неравенств, указываются стрелками, направленными в сторону допустимых значений переменных.
Полученное таким образом пространство решений - многоугольник ABCDEF(показан на рис. 1.)
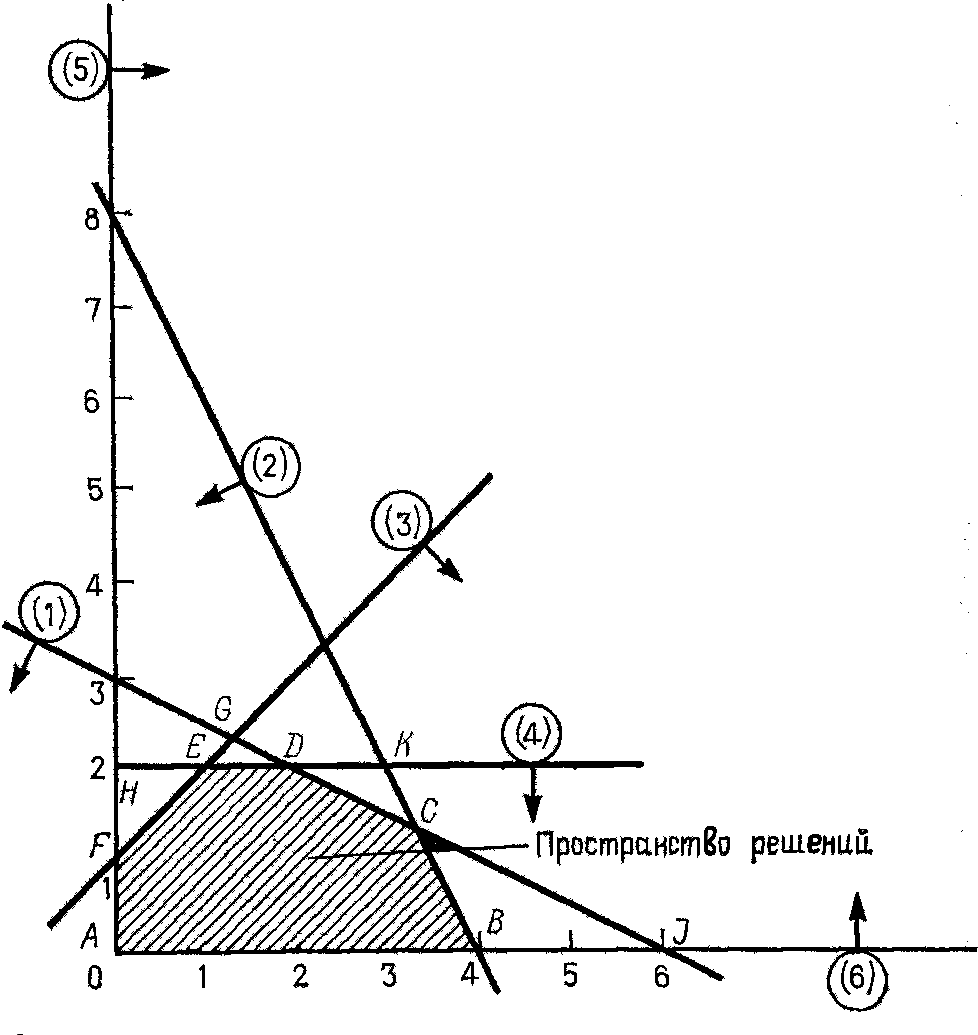
Рис. 1. Ограничения:
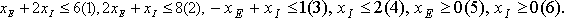
В каждой точке, принадлежащей внутренней области или границам многоугольника решений ABCDEF, все ограничения выполняются, поэтому решения, соответствующие этим точкам, являются допустимыми.
Пространство решений содержит бесконечное число таких точек, но несмотря на это, можно найти оптимальное решение, если выяснить, в каком направлении возрастает целевая функция модели
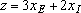 Для этого (рис. 2) на график наносят ряд параллельных линий, соответствующих уравнению целевой функции при нескольких произвольно выбранных и последовательно возрастающих значениях z
z=6 и z=9, что позволяет определить наклон целевой функции и направление, в котором происходит ее увеличение (т. е. возрастание общего дохода)
Для этого (рис. 2) на график наносят ряд параллельных линий, соответствующих уравнению целевой функции при нескольких произвольно выбранных и последовательно возрастающих значениях z
z=6 и z=9, что позволяет определить наклон целевой функции и направление, в котором происходит ее увеличение (т. е. возрастание общего дохода)
Чтобы найти оптимальное решение, следует перемещать прямую, характеризующую доход, в направлении возрастания целевой функции до тех пор, пока она не сместится в область недопустимых решений.
Из рис.2 видно, что оптимальному решению соответствует точка С. Так как точка С является точкой пересечения прямых (1)и (2) (рис.2), то
значения хЕ и xI в этой точке определяются решением системы уравнений:
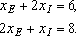
Можно показать, что
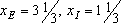 Полученное решение означает, что суточный объем производства краски Е должен быть равен 3.1/3 т, а краски I - 3.1/3 т.
Полученное решение означает, что суточный объем производства краски Е должен быть равен 3.1/3 т, а краски I - 3.1/3 т.
Доход, получаемый в этом случае, составит
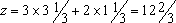 тыс. долл.
тыс. долл.
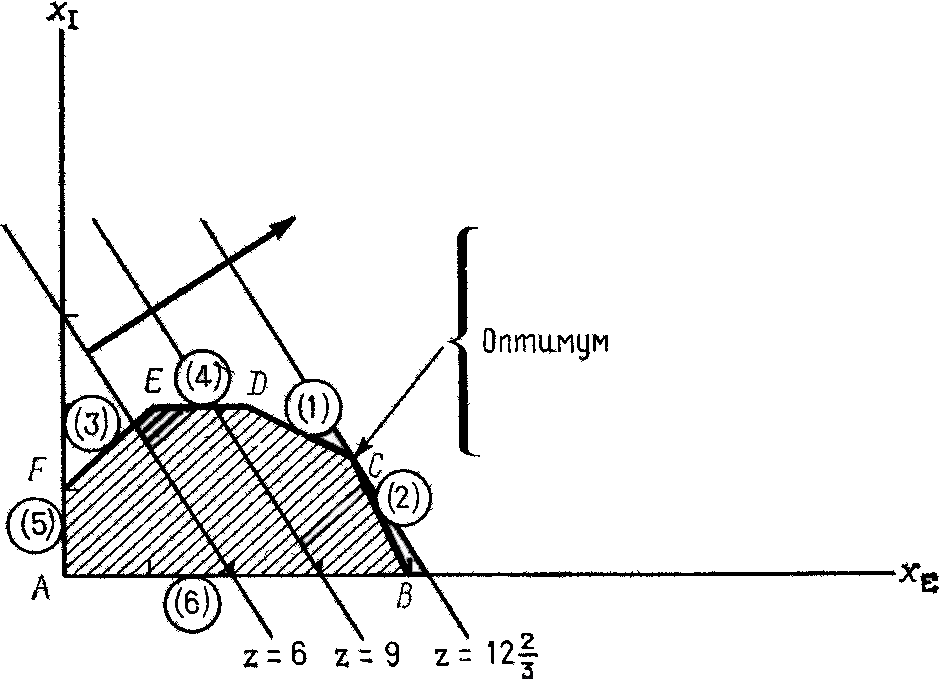
Рис.2.
Целевая функция: максимизировать
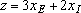 Оптимальное решение:
Оптимальное решение:
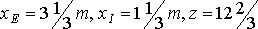 Графическое решение задачи линейного программирования возможно только в частном случае при условии m=n-2. Здесь n - число переменных, m - число уравнений.
Графическое решение задачи линейного программирования возможно только в частном случае при условии m=n-2. Здесь n - число переменных, m - число уравнений.
Отметим некоторые свойства решений ОЗЛП, которые вытекают из геометрических построений и будут иметь место при n-m=2.
- Решение ОЗЛП, если оно существует, не может лежать внутри области допустимых решений, а только на ее границе.
- Решение ОЗЛП может быть и не единственным (см. рис. 3).
Действительно, если основная прямая параллельна той стороне многоугольника допустимых решений, где достигается минимум L', то он достигается не в одной точке, а на всей этой стороне. В этом случае ОЗЛП имеет бесчисленное множество оптимальных решений.
- ОЗЛП может не иметь решения даже в случае, когда существует ОДР (рис. 4)
Это бывает тогда, когда в направлении стрелок ОДР неограничена, т. е. в области допустимых решений линейная функция L неограничена снизу. Перемещая основную прямую в направлении стрелок, мы будем получать все меньшие и меньшие значения L', а значит, и L.
- Решение ОЗЛП, минимизирующее функцию L (оптимальное решение), всегда достигается в одной из вершин многоугольника допустимых решений
{если оно достигается на целой стороне, то оно же достигается и в каждой из вершин, через которые проходит эта сторона).
Решение, лежащее в одной из вершин ОДР, называется опорным решением, а сама вершина-опорной точкой.
- Для того, чтобы найти оптимальное решение, в принципе достаточно перебрать все вершины ОДР (опорные точки) и выбрать из них ту, где функция L достигает минимума.
- Если число свободных переменных в ОЗЛП равно n, а число базисных - т и решение ОЗЛП существует, то оно всегда достигается в точке, где по крайней мере две из переменных x1,x2,...xn обращаются в нуль.
Действительно, в любой опорной точке пересекаются, по крайней мере две из ограничивающих прямых; однако в ней могут пересекаться и более двух (см. рис. 5).
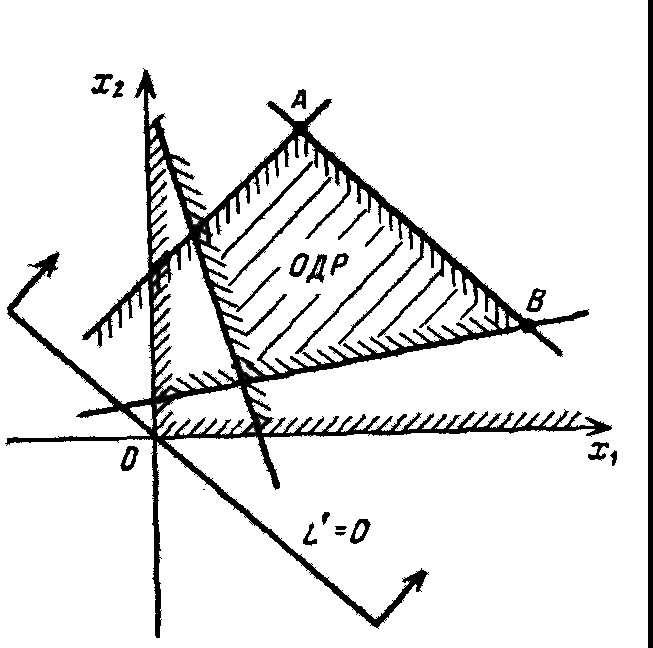
Рис.3.
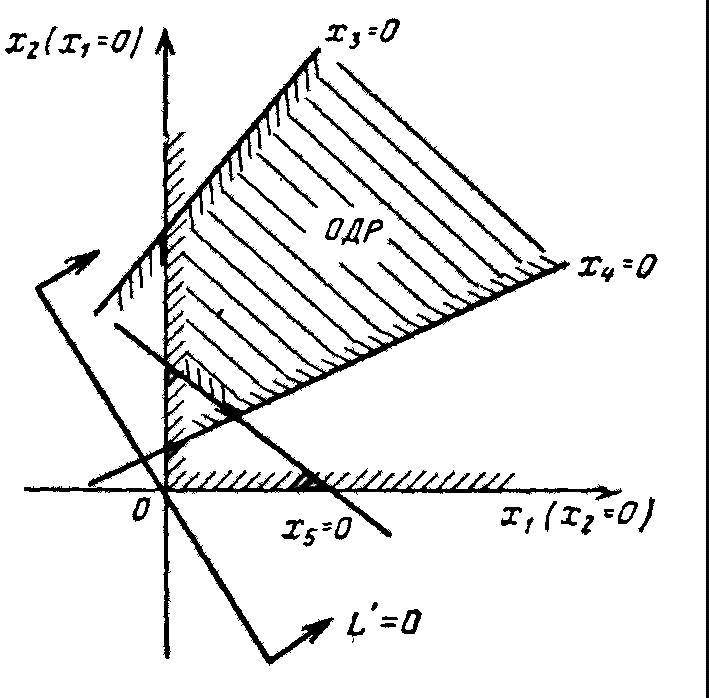
Рис.4.
Случай, когда в оптимальном решении обращаются в нуль не две, а больше переменных, называется вырожденным. На рис. 5 показан вырожденный случай, когда в точке А, соответствующей оптимальному решению, обращаются в нуль три переменные:
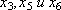
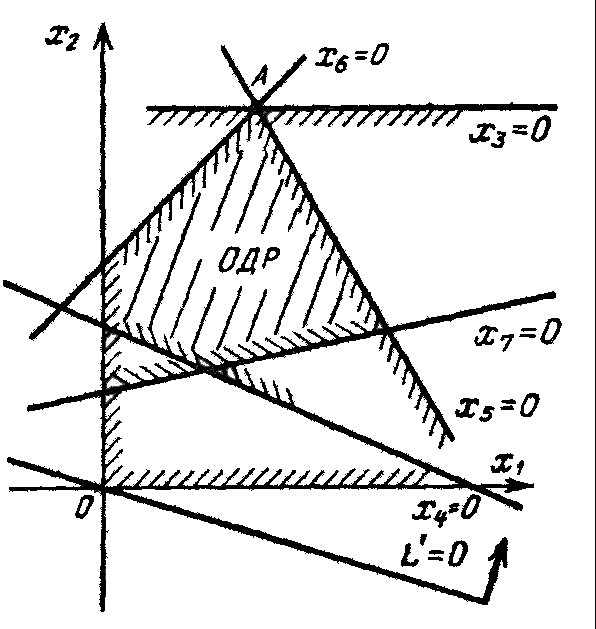
Рис.5.






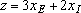
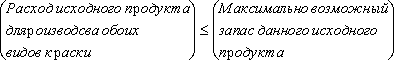
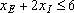 (для А)
(для А)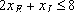 (для В)
(для В)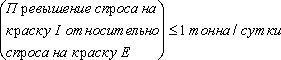
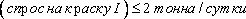
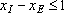 (соотношение величин спроса на краску I и краску Е),
(соотношение величин спроса на краску I и краску Е), 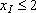 (максимальная величина спроса на краску I).
(максимальная величина спроса на краску I).
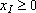 (объем производства краски I),
(объем производства краски I), 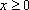 (объем производства краски Е).
(объем производства краски Е).
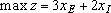 (целевая функция)
(целевая функция)
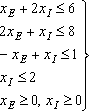
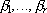 Запасы и потребности сбалансированы, т. е.
Запасы и потребности сбалансированы, т. е.
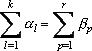 и каждый
и каждый
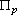 может взаимодействовать с каждым.
Стоимость перевозки единицы имеющегося продукта со склада
может взаимодействовать с каждым.
Стоимость перевозки единицы имеющегося продукта со склада
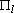 в пункт
в пункт
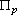 составляет clp.
составляет clp.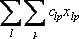 Требуется выбрать такие значения xlp, т. е. составить план перевозок, при которых суммарные затраты на транспортировку окажутся минимальными.
Требуется выбрать такие значения xlp, т. е. составить план перевозок, при которых суммарные затраты на транспортировку окажутся минимальными.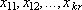 доставляющие минимум функции
доставляющие минимум функции
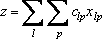 при ограничениях:
при ограничениях:
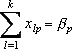 (каждый пункт потребления получает нужное количество продукта);
(каждый пункт потребления получает нужное количество продукта);
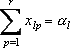 (каждый склад полностью освобождается);
(каждый склад полностью освобождается);
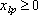 (объемы перевозок не могут быть отрицательными).
(объемы перевозок не могут быть отрицательными).
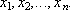 Требуется найти такие их неотрицательные значения, которые удовлетворяли бы системе линейных уравнений:
Требуется найти такие их неотрицательные значения, которые удовлетворяли бы системе линейных уравнений: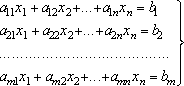 {1}
{1}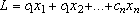 Очевидно, случай, когда линейную функцию нужно обратить не в минимум, а в максимум, легко сводится к предыдущему, если изменить знак функции и рассмотреть вместо нее функцию
Очевидно, случай, когда линейную функцию нужно обратить не в минимум, а в максимум, легко сводится к предыдущему, если изменить знак функции и рассмотреть вместо нее функцию
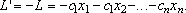 Оптимальным решением будем называть то из допустимых решений, при котором линейная функция обращается в минимум.
Оптимальным решением будем называть то из допустимых решений, при котором линейная функция обращается в минимум.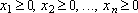 удовлетворяющую уравнениям (1).
удовлетворяющую уравнениям (1).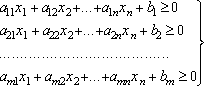
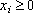 которые удовлетворяют неравенствам и обращают в минимум
которые удовлетворяют неравенствам и обращают в минимум
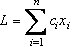 {2}
{2}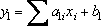
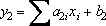 {3}
{3}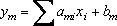
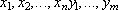 чтобы они удовлетворяли системе уравнений (3) и обращали в минимум
чтобы они удовлетворяли системе уравнений (3) и обращали в минимум
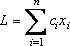 Коэффициенты в формуле (2) перед yj равны нулю.
Коэффициенты в формуле (2) перед yj равны нулю.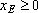 и
и
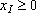 ограничивают область их
допустимых значений первым квадрантом.
ограничивают область их
допустимых значений первым квадрантом. 
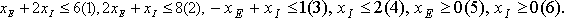
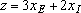 Для этого (рис. 2) на график наносят ряд параллельных линий, соответствующих уравнению целевой функции при нескольких произвольно выбранных и последовательно возрастающих значениях z
z=6 и z=9, что позволяет определить наклон целевой функции и направление, в котором происходит ее увеличение (т. е. возрастание общего дохода)
Для этого (рис. 2) на график наносят ряд параллельных линий, соответствующих уравнению целевой функции при нескольких произвольно выбранных и последовательно возрастающих значениях z
z=6 и z=9, что позволяет определить наклон целевой функции и направление, в котором происходит ее увеличение (т. е. возрастание общего дохода) 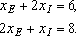
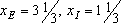 Полученное решение означает, что суточный объем производства краски Е должен быть равен 3.1/3 т, а краски I - 3.1/3 т.
Полученное решение означает, что суточный объем производства краски Е должен быть равен 3.1/3 т, а краски I - 3.1/3 т. 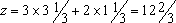 тыс. долл.
тыс. долл.

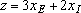 Оптимальное решение:
Оптимальное решение:
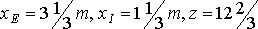 Графическое решение задачи линейного программирования возможно только в частном случае при условии m=n-2. Здесь n - число переменных, m - число уравнений.
Графическое решение задачи линейного программирования возможно только в частном случае при условии m=n-2. Здесь n - число переменных, m - число уравнений.